Calculatrice de fonction d'erreur complémentaire

Calculez la fonction d'erreur complémentaire.

Embed Calculatrice de fonction d'erreur complémentaire Widget

Calculatrice de fonction d'erreur complémentaire

Le Calculateur de fonction d'erreur complémentaire permet de calculer la fonction d'erreur complémentaire d'un nombre donné.

Fonction d'erreur complémentaire

En mathématiques, la fonction d'erreur complémentaire (aussi appelée fonction d'erreur complémentaire de Gauss) est définie comme :

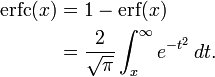
Table de fonctions d'erreur complémentaire

Le tableau suivant présente la fonction d'erreur et la fonction d'erreur complémentaire qui montre les valeurs de erf(x) et erfc(x) pour x allant de 0 à 3,5 avec un incrément de 0,01.

X	erf (x)	erfc (x)
0.0	0.0	1,0
0,01	0.011283416	0,988716584
0,02	0.022564575	0,977435425
0,03	0.033841222	0,966158778
0,04	0.045111106	0.954888894
0,05	0,056371978	0,943628022
0,06	0.067621594	0,932378406
0,07	0,07885772	0,92114228
0,08	0.090078126	0.909921874
0,09	0,101280594	0.898719406
0,1	0.112462916	0.887537084
0,11	0,123622896	0.876377104
0,12	0.134758352	0.865241648
0,13	0.145867115	0.854132885
0,14	0,156947033	0.843052967
0,15	0.167995971	0.832004029
0,16	0,179011813	0.820988187
0,17	0,189992461	0.810007539
0,18	0.200935839	0.799064161
0,19	0.211839892	0,788160108
0,2	0.222702589	0,777297411
0,21	0.233521923	0,766478077
0,22	0.244295912	0,755704088
0,23	0.2550226	0,7449774
0.24	0,265700059	0,734299941
0,25	0.27632639	0,72367361
0,26	0,286899723	0,713100277
0,27	0.297418219	0,702581781
0,28	0,307880068	0,692119932
0,29	0.318283496	0.681716504
0,3	0,328626759	0,671373241
0,31	0,33890815	0,66109185
0,32	0.349125995	0.650874005
0,33	0,359278655	0.640721345
0,34	0,369364529	0.630635471
0,35	0.379382054	0.620617946
0,36	0,389329701	0.610670299
0,37	0.399205984	0.600794016
0,38	0.409009453	0.590990547
0,39	0,4187387	0.5812613
0.4	0,428392355	0.571607645
0,41	0.43796909	0.56203091
0.42	0.447467618	0.552532382
0.43	0,456886695	0.543113305
0,44	0.466225115	0.533774885
0,45	0.47548172	0.52451828
0,46	0,48465539	0.51534461
0,47	0.493745051	0.506254949
0,48	0.502749671	0.497250329
0,49	0.511668261	0,488331739
0.5	0.520499878	0.479500122
0,51	0.52924362	0.47075638
0,52	0.53789863	0.46210137
0,53	0.546464097	0.453535903
0,54	0.55493925	0.44506075
0,55	0.563323366	0,436676634
0,56	0.571615764	0.428384236
0,57	0.579815806	0.420184194
0,58	0.5879229	0.4120771
0,59	0.595936497	0.404063503
0.6	0.603856091	0.396143909
0,61	0,611681219	0,388318781
0,62	0,619411462	0.380588538
0,63	0.627046443	0,372953557
0,64	0.634585829	0.365414171
0,65	0.642029327	0,357970673
0,66	0,649376688	0.350623312
0,67	0.656627702	0,343372298
0,68	0.663782203	0,336217797
0,69	0.670840062	0.329159938
0,7	0,677801194	0.322198806
0,71	0,68466555	0,31533445
0,72	0.691433123	0,308566877
0,73	0,698103943	0,301896057
0,74	0,704678078	0.295321922
0,75	0,711155634	0,288844366
0,76	0,717536753	0,282463247
0,77	0,723821614	0.276178386
0,78	0,730010431	0.269989569
0,79	0,736103454	0.263896546
0.8	0.742100965	0.257899035
0,81	0,748003281	0.251996719
0,82	0.753810751	0.246189249
0,83	0,759523757	0.240476243
0,84	0,765142711	0.234857289
0,85	0,770668058	0.229331942
0,86	0,776100268	0.223899732
0,87	0,781439845	0.218560155
0,88	0,786687319	0.213312681
0,89	0.791843247	0,208156753
0,9	0,796908212	0.203091788
0,91	0.801882826	0.198117174
0,92	0.806767722	0,193232278
0,93	0.811563559	0.188436441
0,94	0.816271019	0,183728981
0.95	0.820890807	0,179109193
0,96	0.82542365	0,17457635
0,97	0.829870293	0,170129707
0,98	0.834231504	0.165768496
0,99	0.83850807	0,16149193
1,0	0.842700793	0,157299207
1,01	0.846810496	0.153189504
1,02	0.850838018	0.149161982
1,03	0.854784211	0.145215789
1.04	0.858649947	0,141350053
1,05	0.862436106	0,137563894
1,06	0.866143587	0.133856413
1,07	0.869773297	0.130226703
1,08	0.873326158	0,126673842
1,09	0.876803102	0.123196898
1.1	0.88020507	0.11979493
1.11	0.883533012	0,116466988
1,12	0.88678789	0.11321211
1,13	0.88997067	0.11002933
1,14	0.893082328	0,106917672
1,15	0.896123843	0,103876157
1,16	0.899096203	0.100903797
1,17	0.902000399	0.097999601
1,18	0.904837427	0.095162573
1,19	0.907608286	0.092391714
1.2	0,910313978	0,089686022
1,21	0,912955508	0,087044492
1,22	0,915533881	0.084466119
1,23	0,918050104	0.081949896
1,24	0,920505184	0,079494816
1,25	0,922900128	0.077099872
1,26	0,925235942	0.074764058
1,27	0,927513629	0.072486371
1,28	0,929734193	0.070265807
1,29	0,931898633	0.068101367
1.3	0,934007945	0.065992055
1,31	0,936063123	0.063936877
1,32	0,938065155	0.061934845
1,33	0.940015026	0.059984974
1,34	0,941913715	0,058086285
1,35	0,943762196	0.056237804
1,36	0,945561437	0.054438563
1,37	0,947312398	0.052687602
1,38	0,949016035	0.050983965
1,39	0,950673296	0.049326704
1.4	0.95228512	0,04771488
1,41	0.953852439	0,046147561
1,42	0,955376179	0.044623821
1,43	0.956857253	0.043142747
1,44	0.95829657	0.04170343
1,45	0.959695026	0.040304974
1,46	0,96105351	0,03894649
1,47	0,9623729	0,0376271
1,48	0,963654065	0.036345935
1,49	0,964897865	0.035102135
1,5	0,966105146	0.033894854
1,51	0,967276748	0.032723252
1,52	0,968413497	0.031586503
1,53	0,969516209	0.030483791
1,54	0,97058569	0.02941431
1,55	0,971622733	0,028377267
1,56	0,972628122	0.027371878
1,57	0,973602627	0.026397373
1,58	0,974547009	0.025452991
1,59	0,975462016	0.024537984
1,6	0,976348383	0.023651617
1,61	0,977206837	0.022793163
1,62	0,978038088	0.021961912
1,63	0,97884284	0.02115716
1,64	0,97962178	0,02037822
1,65	0,980375585	0.019624415
1,66	0,981104921	0.018895079
1,67	0,981810442	0.018189558
1,68	0,982492787	0.017507213
1,69	0,983152587	0.016847413
1,7	0,983790459	0.016209541
1,71	0,984407008	0.015592992
1,72	0,985002827	0.014997173
1,73	0,9855785	0,0144215
1,74	0,986134595	0.013865405
1,75	0,986671671	0.013328329
1,76	0,987190275	0,012809725
1,77	0,987690942	0.012309058
1,78	0,988174196	0.011825804
1,79	0,988640549	0.011359451
1.8	0,989090502	0.010909498
1,81	0,989524545	0.010475455
1,82	0,989943156	0.010056844
1,83	0,990346805	0.009653195
1,84	0,990735948	0.009264052
1,85	0,99111103	0,00888897
1,86	0,991472488	0.008527512
1,87	0,991820748	0.008179252
1,88	0,992156223	0.007843777
1,89	0,992479318	0.007520682
1,9	0,992790429	0.007209571
1,91	0,99308994	0.00691006
1,92	0,993378225	0.006621775
1,93	0,99365565	0.00634435
1,94	0,993922571	0.006077429
1,95	0,994179334	0.005820666
1,96	0,994426275	0.005573725
1,97	0,994663725	0.005336275
1,98	0,994892	0,005108
1,99	0,995111413	0.004888587
2.0	0,995322265	0.004677735
2.01	0,995524849	0.004475151
2.02	0,995719451	0.004280549
2.03	0,995906348	0.004093652
2.04	0,99608581	0.00391419
2,05	0,996258096	0.003741904
2,06	0,996423462	0.003576538
2,07	0,996582153	0.003417847
2,08	0,996734409	0.003265591
2,09	0,996880461	0.003119539
2.1	0,997020533	0.002979467
2.11	0,997154845	0.002845155
2.12	0,997283607	0.002716393
2.13	0,997407023	0.002592977
2.14	0,997525293	0.002474707
2,15	0,997638607	0.002361393
2,16	0,997747152	0.002252848
2,17	0,997851108	0.002148892
2,18	0,997950649	0.002049351
2,19	0,998045943	0.001954057
2.2	0,998137154	0.001862846
2,21	0,998224438	0.001775562
2,22	0,998307948	0.001692052
2,23	0,998387832	0.001612168
2.24	0,998464231	0.001535769
2,25	0,998537283	0.001462717
2,26	0,998607121	0.001392879
2,27	0,998673872	0.001326128
2,28	0,998737661	0.001262339
2,29	0,998798606	0.001201394
2.3	0,998856823	0.001143177
2,31	0,998912423	0.001087577
2,32	0,998965513	0.001034487
2,33	0,999016195	0.000983805
2,34	0,99906457	0.00093543
2,35	0,999110733	0.000889267
2,36	0,999154777	0.000845223
2,37	0,99919679	0.00080321
2,38	0,999236858	0.000763142
2,39	0,999275064	0.000724936
2.4	0,999311486	0.000688514
2,41	0,999346202	0.000653798
2,42	0,999379283	0.000620717
2,43	0,999410802	0.000589198
2,44	0,999440826	0.000559174
2,45	0,99946942	0.00053058
2,46	0,999496646	0.000503354
2,47	0,999522566	0.000477434
2,48	0,999547236	0.000452764
2,49	0,999570712	0.000429288
2,5	0,999593048	0.000406952
2,51	0,999614295	0.000385705
2,52	0,999634501	0.000365499
2,53	0,999653714	0.000346286
2,54	0,999671979	0.000328021
2,55	0,99968934	0.00031066
2,56	0,999705837	0.000294163
2,57	0,999721511	0.000278489
2,58	0,9997364	0.0002636
2,59	0,999750539	0.000249461
2.6	0,999763966	0.000236034
2,61	0,999776711	0.000223289
2,62	0,999788809	0.000211191
2,63	0,999800289	0.000199711
2,64	0,999811181	0.000188819
2,65	0,999821512	0.000178488
2,66	0,999831311	0.000168689
2,67	0,999840601	0.000159399
2,68	0,999849409	0.000150591
2,69	0,999857757	0.000142243
2,7	0,999865667	0.000134333
2,71	0,999873162	0.000126838
2,72	0,999880261	0.000119739
2,73	0,999886985	0.000113015
2,74	0,999893351	0.000106649
2,75	0,999899378	0.000100622
2,76	0,999905082	9.4918e-05
2,77	0,99991048	8.952e-05
2,78	0,999915587	8.4413e-05
2,79	0,999920418	7.9582e-05
2.8	0,999924987	7.5013e-05
2,81	0,999929307	7.0693e-05
2,82	0,99993339	6.661e-05
2,83	0,99993725	6.275e-05
2,84	0,999940898	5.9102e-05
2,85	0,999944344	5.5656e-05
2,86	0,999947599	5.2401e-05
2,87	0,999950673	4.9327e-05
2,88	0,999953576	4.6424e-05
2,89	0,999956316	4.3684e-05
2,9	0,999958902	4.1098e-05
2,91	0,999961343	3.8657e-05
2,92	0,999963645	3.6355e-05
2,93	0,999965817	3.4183e-05
2,94	0,999967866	3.2134e-05
2,95	0,999969797	3.0203e-05
2,96	0,999971618	2.8382e-05
2,97	0,999973334	2.6666e-05
2,98	0,999974951	2.5049e-05
2,99	0,999976474	2.3526e-05
3.0	0,99997791	2.209e-05
3.01	0,999979261	2.0739e-05
3.02	0,999980534	1.9466e-05
3.03	0,999981732	1.8268e-05
3.04	0,999982859	1.7141e-05
3.05	0,99998392	1.608e-05
3.06	0,999984918	1.5082e-05
3.07	0,999985857	1.4143e-05
3.08	0,99998674	1.326e-05
3.09	0,999987571	1.2429e-05
3.1	0,999988351	1.1649e-05
3.11	0,999989085	1.0915e-05
3.12	0,999989774	1.0226e-05
3.13	0,999990422	9.578e-06
3.14	0,99999103	8.97e-06
3.15	0,999991602	8.398e-06
3.16	0,999992138	7.862e-06
3.17	0,999992642	7.358e-06
3.18	0,999993115	6.885e-06
3.19	0,999993558	6.442e-06
3.2	0,999993974	6.026e-06
3.21	0,999994365	5.635e-06
3.22	0,999994731	5.269e-06
3.23	0,999995074	4.926e-06
3.24	0,999995396	4.604e-06
3,25	0,999995697	4.303e-06
3.26	0,99999598	4.02e-06
3,27	0,999996245	3.755e-06
3,28	0,999996493	3.507e-06
3.29	0,999996725	3.275e-06
3.3	0,999996942	3.058e-06
3,31	0,999997146	2.854e-06
3,32	0,999997336	2.664e-06
3,33	0,999997515	2.485e-06
3,34	0,999997681	2.319e-06
3,35	0,999997838	2.162e-06
3,36	0,999997983	2.017e-06
3,37	0,99999812	1.88e-06
3,38	0,999998247	1.753e-06
3,39	0,999998367	1.633e-06
3.4	0,999998478	1.522e-06
3,41	0,999998582	1.418e-06
3,42	0,999998679	1.321e-06
3,43	0,99999877	1.23e-06
3,44	0,999998855	1.145e-06
3,45	0,999998934	1.066e-06
3,46	0,999999008	9.92e-07
3,47	0,999999077	9.23e-07
3,48	0,999999141	8.59e-07
3,49	0,999999201	7.99e-07
3,5	0,999999257	7.43e-07

Reference this content, page, or tool as:

"Calculatrice de fonction d'erreur complémentaire" at https://miniwebtool.com/fr/complementary-error-function-calculator/ from miniwebtool, https://miniwebtool.com/

You can also try our new AI Math Solver to solve your math problems through natural language question and answer.

Autres outils connexes:

Calculatrice de fonction d'erreur

Calculatrice de fonction d'erreur complémentaire